图形学入门–变换

最近在学图形学，并顺手学个rust，用rust来做一个shader，实践之前需要在课后再深入复习一下。 图形学我看的是闫令琪大神的GAMES101: 现代计算机图形学入门,想要学习的话可以看看,视频在B站上也很方便.

由于我是个初学者, 一年前开始接触unity3D和blender这些软件, 对三维世界有大致的了解, 因此会在我之前的理解上进行复盘. 同时一些示例图片会通过blender生成.

向量变换

区别于图片的像素矩阵, 图形学的世界更类似于数学方程式. 对一个模型的描述, 通常使用由无数个三角形组成的面来表示, 将三角形分解, 就是三个点.

image-20210509101259239

对于点的描述可以表示成 $[x,y]^T$​ , 上面的转置是由于在图形学中一般点和向量习惯竖着写$$\left[ \begin{matrix} x\\ y \end{matrix} \right]$$

以下为四个点围成的正方形, 其中x和y都为1, $$\left[\begin{matrix} 1\\ 1 \end{matrix} \right]$$ ,并将其放到笛卡尔坐标系中.

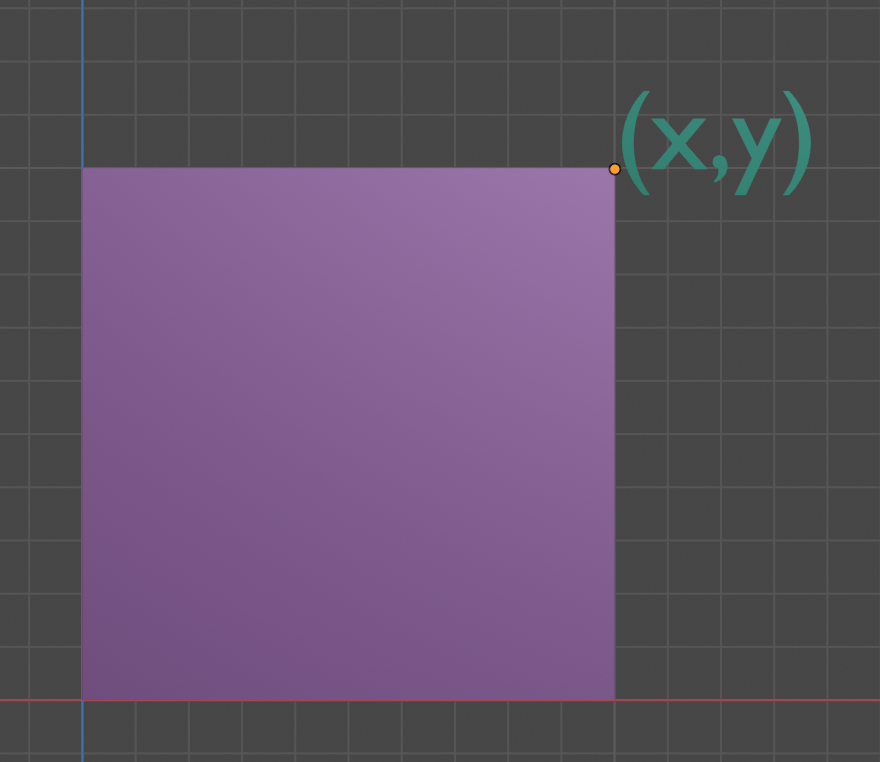
image-20210509103739566

此时我们可以对做以下操作:

  • 线性变换
    • 基于原点的缩放 $$\left[\begin{matrix} x’\\ y' \end{matrix} \right] = S_{(x,y)}\cdot\left[\begin{matrix} x\\ y \end{matrix} \right] = \left[\begin{matrix} s_x & 0\\ 0 & s_y \end{matrix} \right]\cdot\left[\begin{matrix} x\\ y \end{matrix} \right]$$
    • 基于原点的旋转 $$\left[\begin{matrix} x’\\ y' \end{matrix} \right] = R_\theta\cdot\left[\begin{matrix} x\\ y \end{matrix} \right] = \left[\begin{matrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{matrix} \right]\cdot\left[\begin{matrix} x\\ y \end{matrix} \right]$$
  • 平移变换
    • 平移 $$\left[\begin{matrix} x’\\ y' \end{matrix} \right] = T_{(x,y)}+\left[\begin{matrix} x\\ y \end{matrix} \right] = \left[\begin{matrix} t_x\\ t_y \end{matrix} \right]+\left[\begin{matrix} x\\ y \end{matrix} \right]$$

一个点的所有变换在笛卡尔坐标系下无法通过线性变换来表示,只能通过仿射变换来表示,就会产生一些麻烦,因此我们引入齐次坐标来将平移变换也转换为线性变换.

齐次坐标

齐次坐标就是通过高维来表示地维的坐标.

  • 二维点: $$\left[\begin{matrix} x \\ y \\ 1 ​ \end{matrix} \right]$$
  • 二维向量: $$\left[\begin{matrix} x \\ y \\ 0 ​ \end{matrix} \right]$$

我们可以看出,点和向量的唯一区别在于$z$是否为0，当$z$为0的时候是向量，为1的时候是点。

可以简单验证一下：

  • vector + vector = vector
  • point - point = point
  • point + vector = point

而 point + point 相加会发现最后一维变成了2，但这个问题不大，在图形学中齐次坐标的点有以下定义：

$$ \left( \begin{matrix} x \\ y \\ \omega \end{matrix} \right) = \left( \begin{matrix} x/\omega \\ y/\omega \\ 1 \end{matrix} \right), \omega\not=0 $$ 因此 point + point = point 也成立。

齐次坐标下的变换

我们同样可以在齐次坐标下进行变换

  • 基于原点的缩放 $$\left [\begin{matrix} x’ \\ y’ \\ 1 \end{matrix} \right] = S_{(x,y)}\cdot\left[\begin{matrix} x \\ y \\ 1 \end{matrix} \right] = \left[\begin{matrix} s_x & 0 & 0\\ 0 & s_y & 0\\ 0 & 0 & 1 \end{matrix} \right]\cdot\left[\begin{matrix} x\\ y\\ 1 \end{matrix} \right]$$
  • 基于原点的旋转 $$\left[\begin{matrix} x’\\ y’\\ 1 \end{matrix} \right] = R_\theta\cdot\left[\begin{matrix} x\\ y\\ 1 \end{matrix} \right] = \left[\begin{matrix} \cos\theta & -\sin\theta & 0\\ \sin\theta & \cos\theta & 0\\ 0 & 0 & 1 \end{matrix} \right]\cdot\left[\begin{matrix} x\\ y\\ 1 \end{matrix} \right]$$
  • 平移 $$\left[\begin{matrix} x’\\ y’\\ 1 \end{matrix} \right] = T_{(x,y)}+\left[\begin{matrix} x\\ y\\ 1 \end{matrix} \right] = \left[\begin{matrix} 1 & 0 & t_x\\ 0 & 1 & t_y\\ 0 & 0 & 1 \end{matrix} \right] \cdot \left[\begin{matrix} x\\ y\\ 1 \end{matrix} \right]$$

这样一来，我们就能把这些变换都通过线性变换来表示了，可以通过连乘的方法来表示一些列变换。

比如我们对为处于原点的方块进行以下操作。

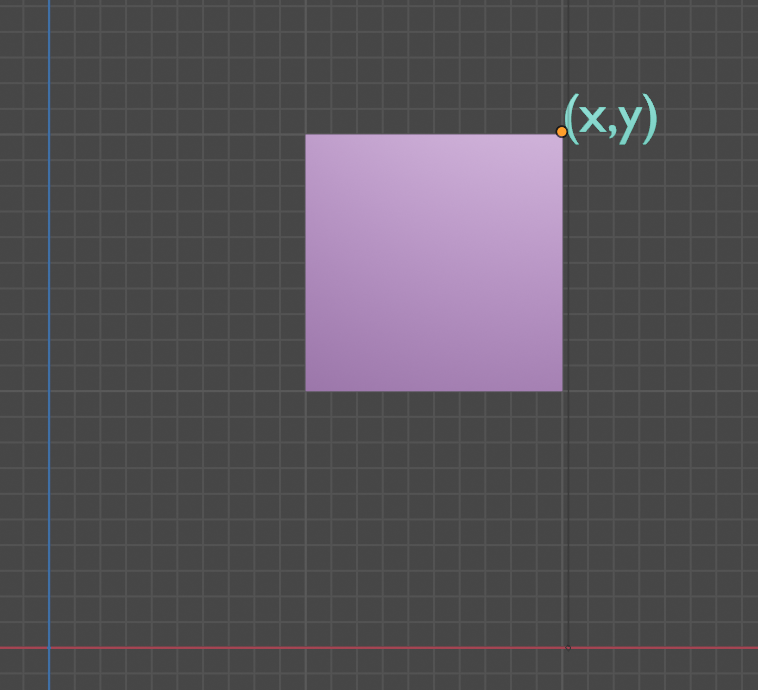$\Longrightarrow$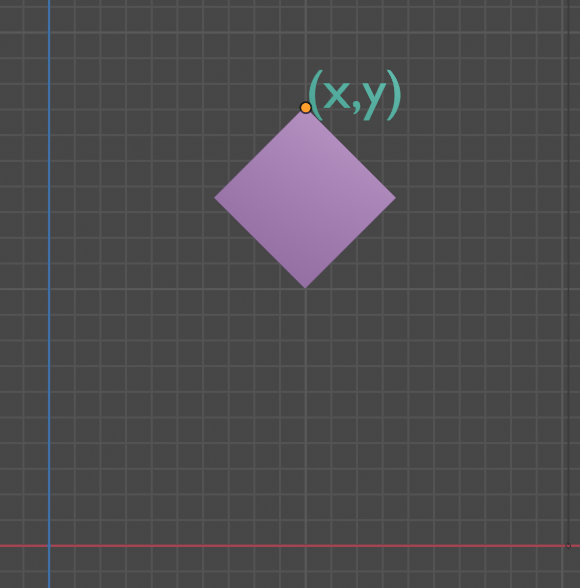

对其进行分析我们可以发现这个变换包含了旋转和缩放，但由于我们上面讲到旋转和缩放都是基于原点的变换，我们无法直接套用上述公式，需要先将其平移至原点做处理后再平移回来。

这需要我们做这样一串操作：

$$T_{(-t_x, -t_y)} \Rightarrow S_{(s_x, s_y)} \Rightarrow R_\theta \Rightarrow T_{(t_x, t_y)}$$

写成公式就是(从右往左运算) $$ p’ = T_{(t_x, t_y)} \cdot R_\theta \cdot S_{(s_x, s_y)} \cdot T_{(-t_x, -t_y)} \cdot p $$ $$ \downarrow $$ $$ \left[ \begin{matrix} x’\\ y’\\ 1 \end{matrix} \right] = \left[\begin{matrix} 1 & 0 & t_x\\ 0 & 1 & t_y\\ 0 & 0 & 1 \end{matrix} \right] \cdot \left[\begin{matrix} \cos\theta & -\sin\theta & 0\\ \sin\theta & \cos\theta & 0\\ 0 & 0 & 1 \end{matrix} \right] \cdot \left[\begin{matrix} s_x & 0 & 0\\ 0 & s_y & 0\\ 0 & 0 & 1 \end{matrix} \right] \cdot \left[\begin{matrix} 1 & 0 & -t_x\\ 0 & 1 & -t_y\\ 0 & 0 & 1 \end{matrix} \right] \cdot \left[\begin{matrix} x\\ y\\ 1 \end{matrix} \right] $$

根据矩阵运算的结合律，我们可以先求 $T_{(t_x, t_y)} \cdot R_\theta \cdot S_{(s_x, s_y)} \cdot T_{(-t_x, -t_y)}$, 减少运算。

此处要注意的是，矩阵运算不符合交换律。

三维变换

三维变换与二维变换类似。

  • 基于原点的缩放 $$\left [\begin{matrix} x’ \\ y’ \\ z’ \\ 1 \end{matrix} \right] = S_{(x,y,z)}\cdot\left[\begin{matrix} x \\ y \\ z \\ 1 \end{matrix} \right] = \left[\begin{matrix} s_x & 0 & 0\\ 0 & s_y & 0\\ 0 & 0 & s_z\\ 0 & 0 & 1 \end{matrix} \right]\cdot\left[\begin{matrix} x\\ y\\ z\\ 1 \end{matrix} \right]$$
  • 平移 $$\left[\begin{matrix} x’\\ y’\\ z’ \\ 1 \end{matrix} \right] = T_{(x,y,z)}+\left[\begin{matrix} x\\ y\\ z\\ 1 \end{matrix} \right] = \left[\begin{matrix} 1 & 0 & 0 & t_x\\ 0 & 1 & 0 & t_y\\ 0 & 0 & 1 & t_z\\ 0 & 0 & 0 & 1 \end{matrix} \right] \cdot \left[\begin{matrix} x\\ y\\ z\\ 1 \end{matrix} \right]$$

但在三维空间中，旋转是特殊的，因为它有三个轴，对每个轴的旋转我们只要忽略这一轴即可：

  • X轴旋转 $$\left[\begin{matrix} x’\\ y’\\ z’ \\ 1 \end{matrix} \right] = R_x\theta\cdot\left[\begin{matrix} x\\ y\\ z \\ 1 \end{matrix} \right] = \left[\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta & 0\\ 0 & \sin\theta & \cos\theta & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right]\cdot\left[\begin{matrix} x\\ y\\ z\\ 1 \end{matrix} \right]$$
  • Y轴旋转 $$\left[\begin{matrix} x’\\ y’\\ z’ \\ 1 \end{matrix} \right] = R_y\theta\cdot\left[\begin{matrix} x\\ y\\ z\\ 1 \end{matrix} \right] = \left[\begin{matrix} \cos\theta & 0 & \sin\theta & 0\\ 0 & 1 & 0 & 0 \\ -\sin\theta & 0 & \cos\theta & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right]\cdot\left[\begin{matrix} x\\ y\\ z\\ 1 \end{matrix} \right]$$
  • Z轴旋转 $$\left[\begin{matrix} x’\\ y’\\ z’ \\ 1 \end{matrix} \right] = R_z\theta\cdot\left[\begin{matrix} x\\ y\\ z \\ 1 \end{matrix} \right] = \left[\begin{matrix} \cos\theta & -\sin\theta & 0 & 0\\ \sin\theta & \cos\theta & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right]\cdot\left[\begin{matrix} x\\ y\\ z\\ 1 \end{matrix} \right]$$

在这里会发现其中Y轴的变换是特殊的，这是由于根据右手螺旋定则，XY可以推出Z，YZ可以推出X，但是XZ推出的是-Y，因此Y相反。

同样我们这边也可以结合三轴旋转变换为： $$R_{xyz}(\alpha\beta\gamma)=R_x(\alpha)R_y(\beta)R_z(\gamma)$$

更复杂一点可以通过罗格里格斯旋转公式求出基于任意从原点出发向量旋转后的点，此处不做展开。