图形学入门–渲染管线
上次大致写了一下变换,那是本文的基础。本次将会对渲染管线做一个比较详细的笔记,大半个月没看图形学了,正好复习一下。
图形学入门–入门 是对 GAMES101: 现代计算机图形学入门 课程的 Lecture 2~3 做了总结,本次将会对 Lecture 4~7 做一个总结。
| 课程名 | 课件链接 | 虎书第四版相应章节 | |
|---|---|---|---|
| Lecture 4 | 变换(模型、视图、投影) | 课件 | 阅读材料:第 6 章(Transformation Matrices),第 6.2、6.4、6.5 节;第 7 章(Viewing) |
| Lecture 5 | 光栅化(三角形的离散化) | 课件 | 阅读材料:第 3 章(Raster Images), 第 3.1、3.2 节 |
| Lecture 6 | 光栅化(深度测试与抗锯齿) | 课件 | 阅读材料:第 8 章(The Graphics Pipeline), 第 8.2.3 节;第 9 章(Signal Processing) |
| Lecture 7 | 着色(光照与基本着色模型) | 课件 | 阅读材料:第 10 章(Surface Shading), 第 10.1 节 |
渲染管线纵览
可以先看看Lecture 8中的渲染管线图。
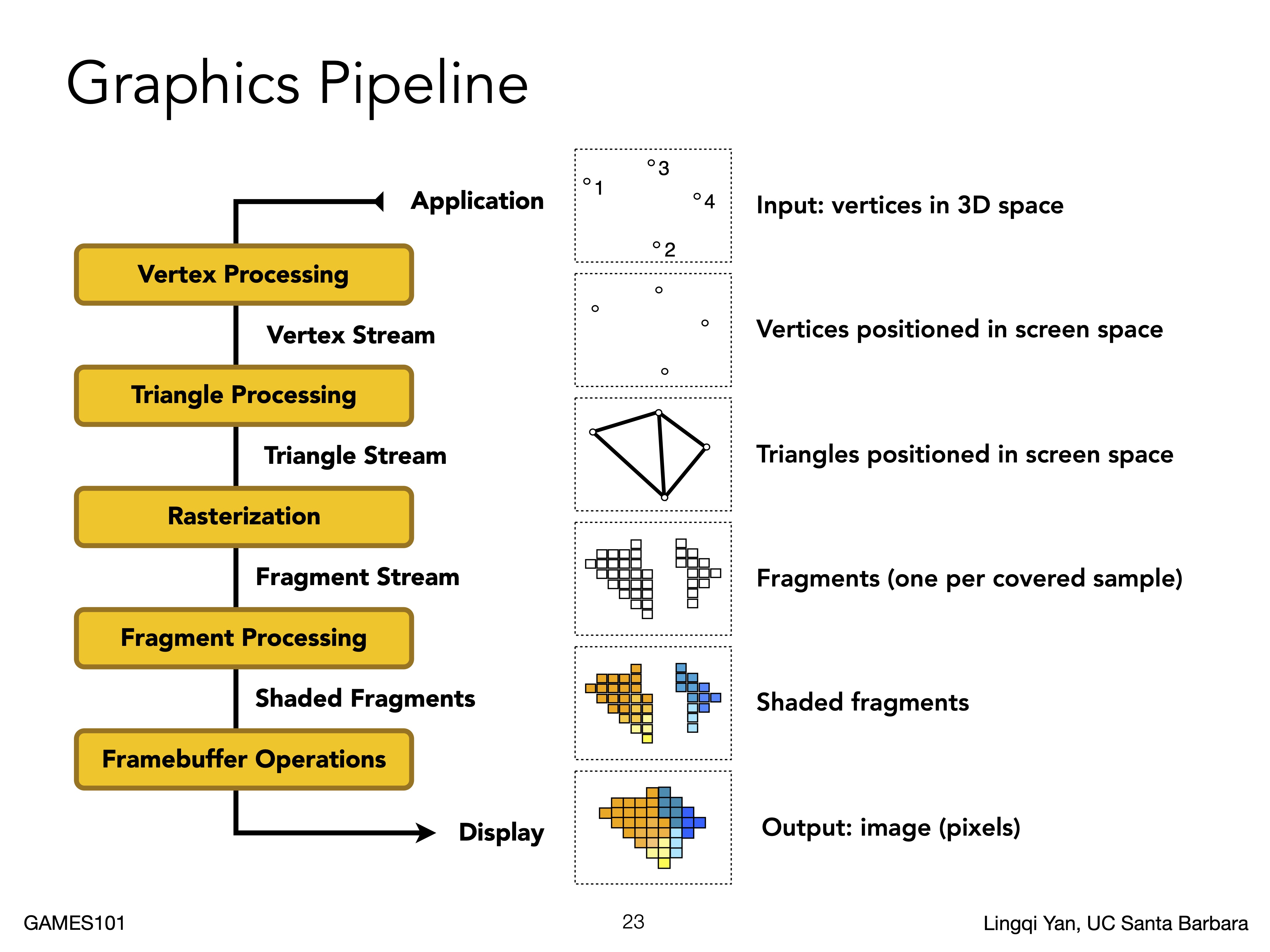
这边的步骤分为
- 点处理
- 三角处理
- 栅格化
- 片元处理
- 片元混合
接下来一步步将模型在图像中画出来
继续回顾变换
虽然在 图形学入门–入门 中已经讲过变换了,但是那仅是针对某个模型围绕原点的变换,但事实上大部分物体不会在原点,并且在场景中会有很多的模型。这一小节变换会回顾一下如何通过变换计算出摄像机所拍摄出的模型。
相机变换
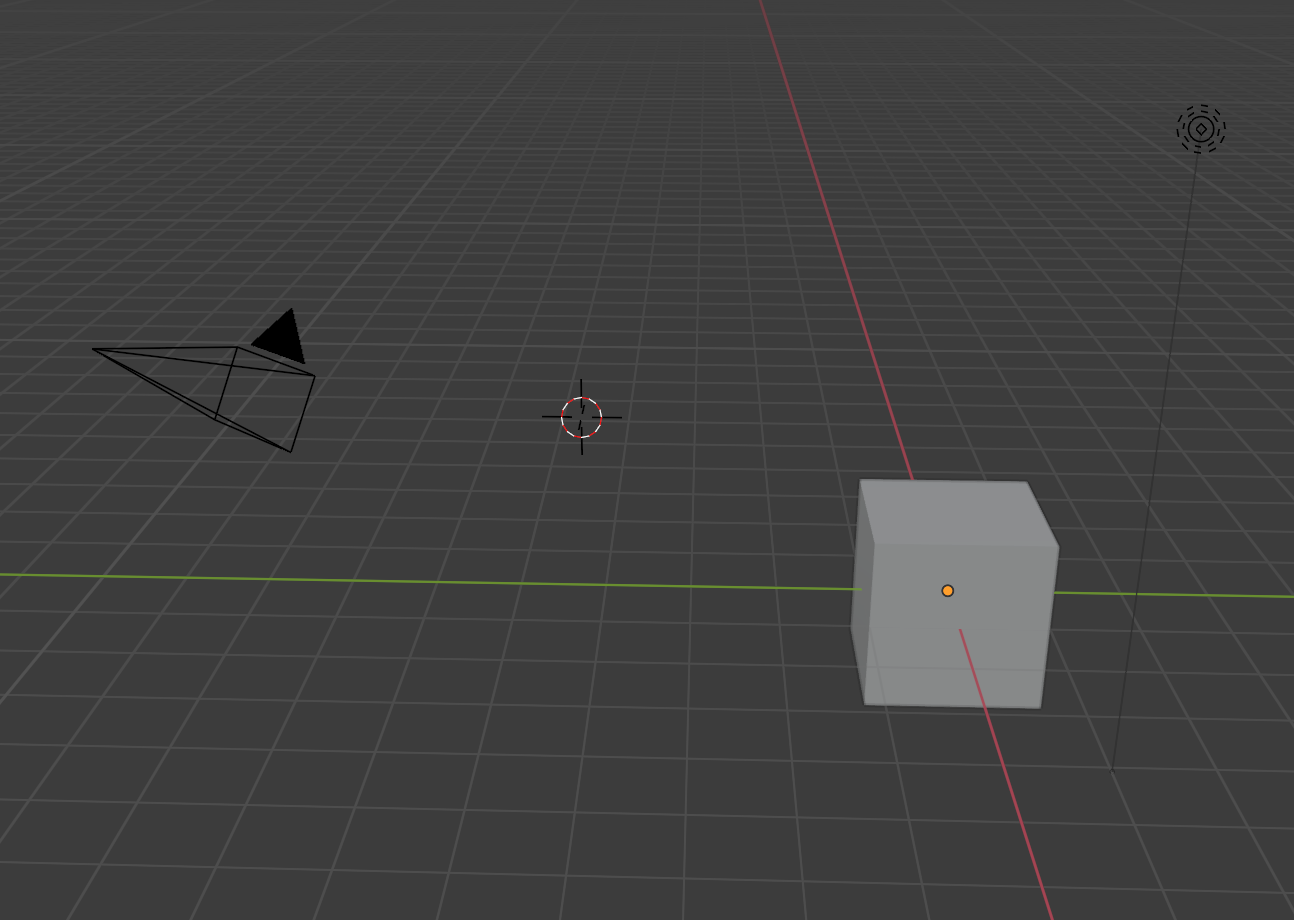
当我们在blender中创建一个工程,会像上图这样自动创建出盒子和摄像机(这边不关心那个光)。对于这样的一个模型很难去做采样,所以通常的做法是将所有需要被拍摄的模型重新放置在以摄像机为原点的坐标上。
摄像机有三个属性:
- 位置(Position $\vec{e}$):这个很容易理解,并且在变换中也提到了位置的概念,即从原点到物体的向量;
- 朝向(Look-at $\hat{g}$):用过游戏引擎的人会对Look-at比较有感受,他是物体面向的方向,对摄像机来说就是摄像机拍摄的方向,需要注意的是这个向量仅代表方向,因此只要是单位向量即可;
- 上方向(Up direction $\hat{t}$):这也是一个单位向量,与look-at共同表示出摄像机完整的朝向信息,他与look-at正交;
通过这三个位置和朝向信息就能来重新计算模型的坐标,让其放在摄像机为原点的坐标上。在 GAMES101: 现代计算机图形学入门 课程中,将up设定为Y轴方向,look at -Z轴方向。(就当下图是对的,用过blender的同学千万不要揭穿我)
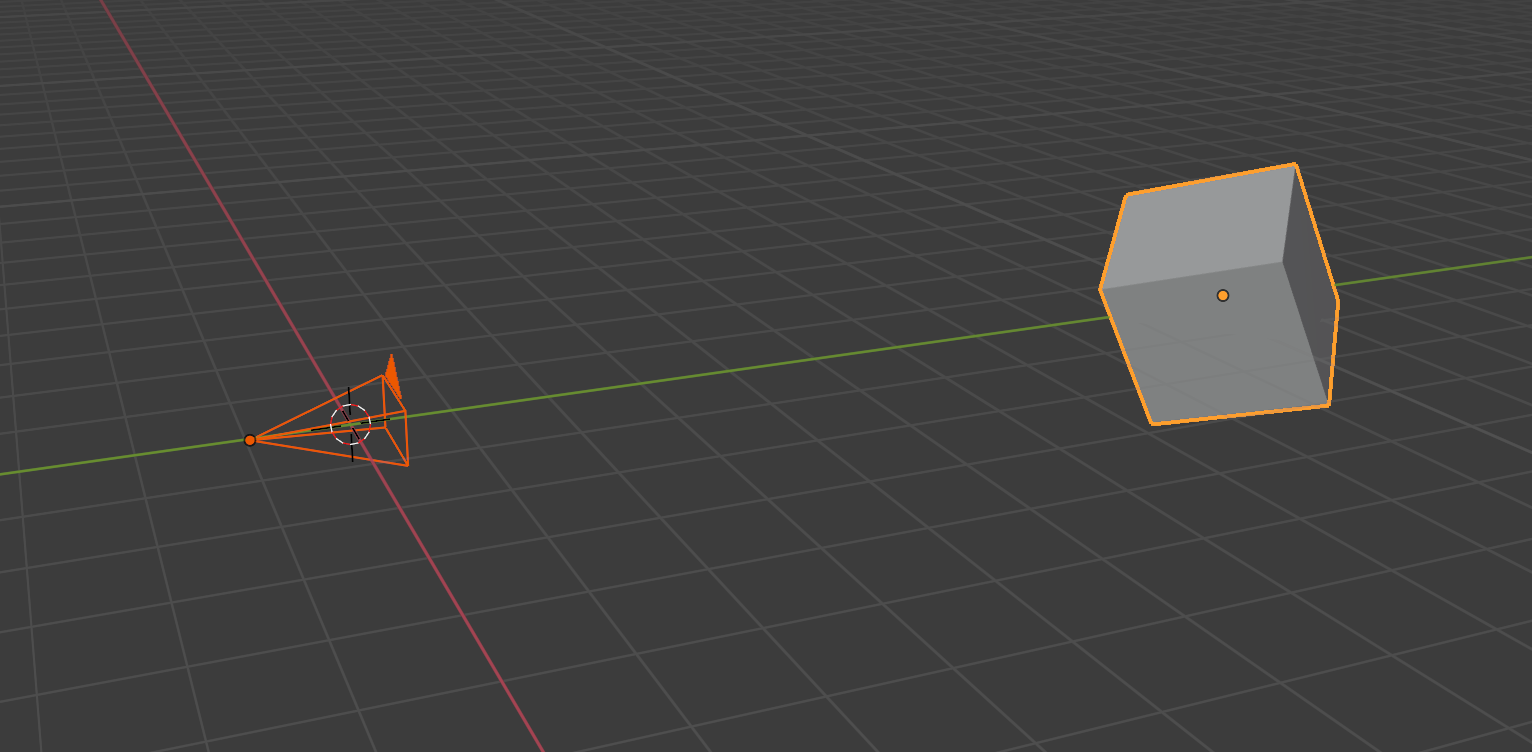
变换矩阵 $M_{view}$ 的计算方式就是:
- 移动 $-\vec{e}$ 到原点;
- 旋转 $\hat{g}$ 到 -Z;
- 旋转 $\hat{t}$ 到 Y;
- 旋转 $(\hat{g}\times\hat{t})$ 到 X。
旋转比较难计算,但是由于旋转是可逆的,并且旋转是正定矩阵( $R_{45} \cdot R_{-45} = I$ 满足正定性,即 $A^TA=I$ , 回顾变换可发现$R_{45}$ 和 $R_{-45}$ 的关系满足转置 ),我们可以先计算以上2~4步的逆矩阵,即
- X 到 $(\hat{g}\times\hat{t})$
- Y 到 $\hat{t}$
- -Z 到 $\hat{g}$
然后再求转置即可。这边懒得写了,直接给结论。
$$ T_{view} = \left[ \begin{matrix} 1 & 0 & 0 & -x_{\vec{e}}\\ 0 & 1 & 0 & -y_{\vec{e}}\\ 0 & 0 & 1 & -z_{\vec{e}}\\ 0 & 0 & 0 & 1 \end{matrix} \right] $$ $$ R_{view} = \left[ \begin{matrix} x_{\hat{g}\times\hat{t}} & y_{\hat{g}\times\hat{t}} & z_{\hat{g}\times\hat{t}} & 0\\ x_{\hat{t}} & y_{\hat{t}} & z_{\hat{t}} & 0\\ x_{-\hat{g}} & y_{-\hat{g}} & z_{-\hat{g}} & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right] $$ $$ M_{view} = R_{view} T_{view} $$
通过相机的变换就能将模型转移到相机为原点的坐标上,再以此进行计算。
投影及物体变换
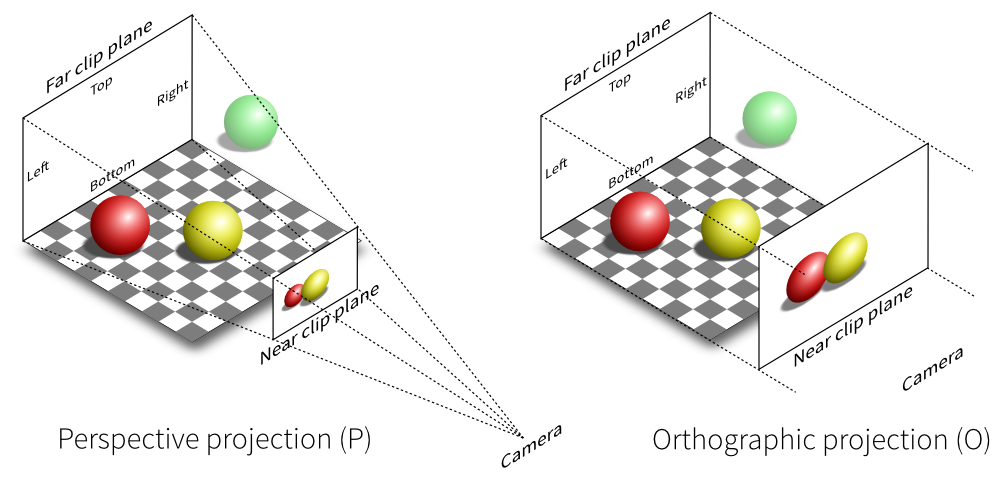
在这边我们可以看到透视投影(左)与正交投影(右)在相机中显示的样子。
从简单的正交投影开始说。正交投影从三维的角度看过去会有一个长方体盒:
- 近平面:摄像机能看到最近的地方,也就是最终生成投影的位置;
- 原平面:摄像机能看到的最远距离,这边我们假设他是有限度的;
- 上下左右四个平面:摄像机的视野范围;
- 宽高比:记得有个属性即可;
这里的的距离单位是长度单位,可能是千米 / 米 / 厘米,但屏幕上是像素点,我们需要进行转换,根据视野的大小一一映射到屏幕像素点上。这边做的处理就是将长方体盒转换成标准立方体,即$[-1,1]^3$ ,然后再根据画面像素扩展到相应大小后再做投影。
这个知识点我在看视频时可能由于是1.5倍速度播放,并没有很好的理解它,上一段文字的理解是在阅读作业框架代码后才明白的。
这一转换就相对简单许多:
$$ M_{ortho} = M_{ortho-scale} \cdot M_{ortho-transform} $$
我们再来看左边的透视投影,他是一个梯形,实际上和正交投影很类似,也有六个面,还外带了一个视场角。我们可以先将透视投影的盒子转为正交投影的盒子,再做正交投影计算就能获得标准立方体。即: $$ M_{persp}=M_{ortho} \cdot M_{persp\rightarrow ortho} $$
这里的 $M_{persp\rightarrow ortho}$ 较为难求,不过也可以推导出来,复习主要是为后续实现rust栅格化渲染器做基础,此处就不做公式推导。直接给出变换矩阵:
$$ M_{persp\rightarrow ortho} = \left[ \begin{matrix} near & 0 & 0 & 0\\ 0 & near & 0 & 0\\ 0 & 0 & near+far & -near\times far\\ 0 & 0 & 1 & 0 \end{matrix} \right] $$
算出模型在标准立方体中的坐标后即可按比例扩大为画面中的像素坐标,再做栅格化。
栅格化
经过一系列变换我们获得了一堆模型坐标点在画面中的位置。
最基础的栅格化算法将多边形表示的三维场景渲染到二维表面。多边形由三角形的集合表示,三角形由三维空间中的三个顶点表示。在最简单的实现形式中,栅格化工具将顶点数据映射到观察者显示器上对应的二维坐标点,然后对变换出的二维三角形进行合适的填充。
—-WikiPedia
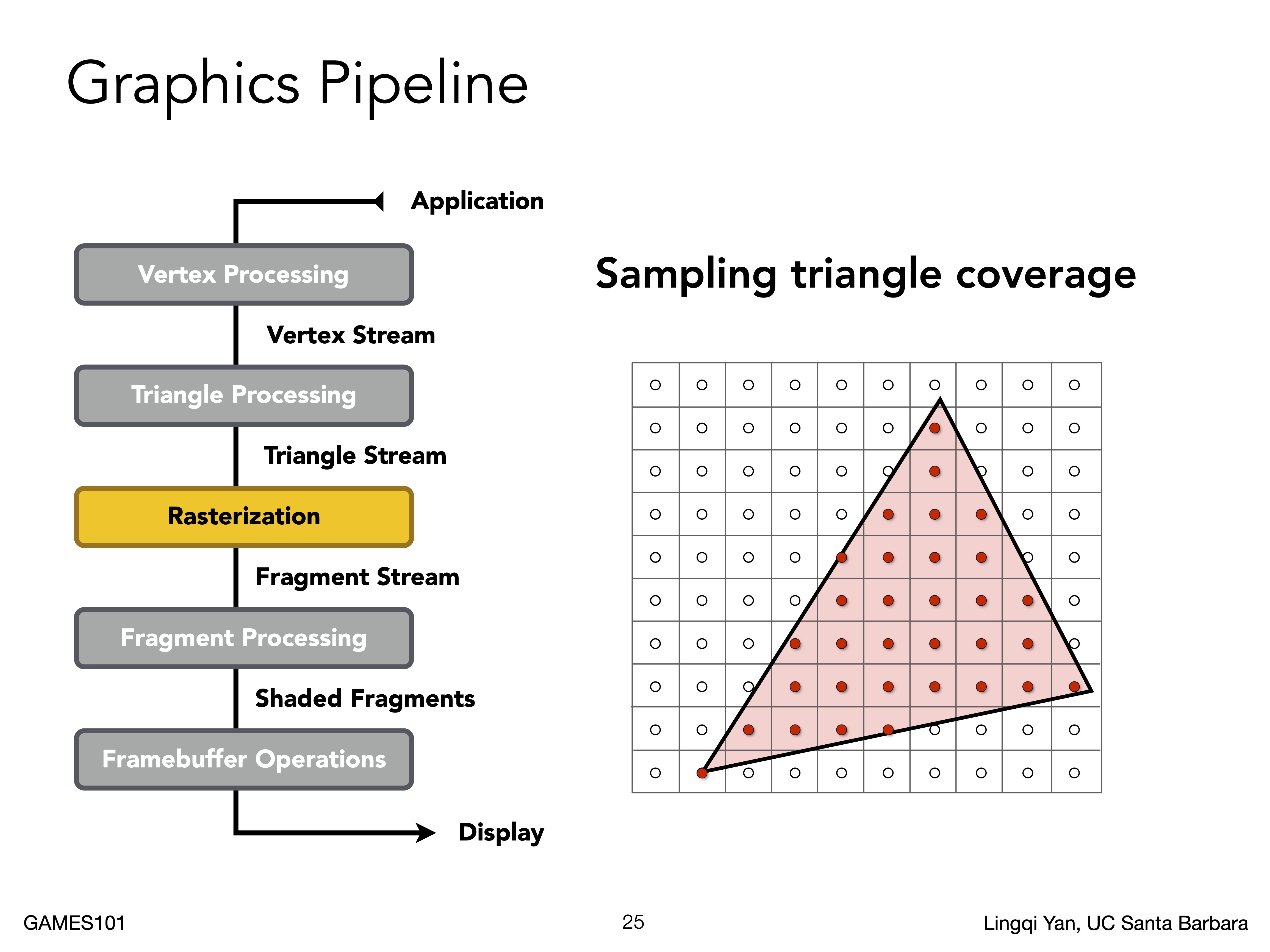
我们需要遍历像素点来判断该点是否在三角形内,在的话就使用该三角形的属性进行渲染。遍历难不倒码农。
但问题在于如何判断点是否在三角形内呢?采用向量叉积的方法来判断。
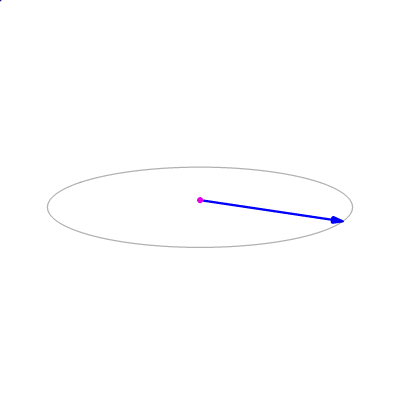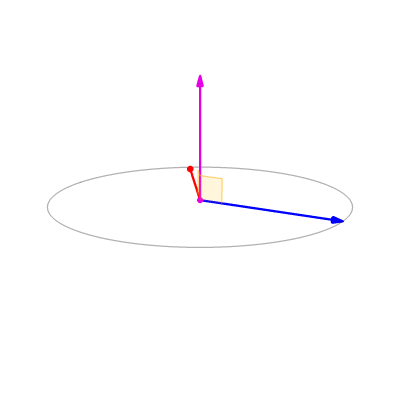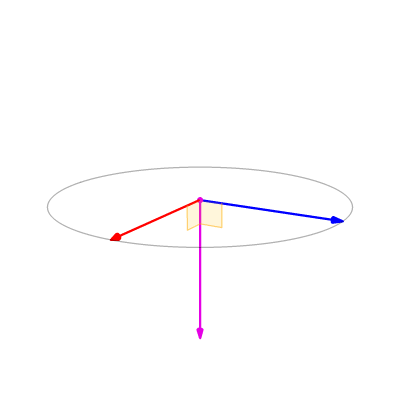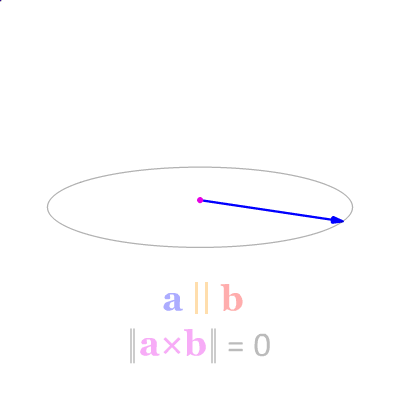
通过叉积可以判断两个向量的左右关系, $\vec{a}\times\vec{b}$ 与 $\vec{b}\times\vec{a}$ 是完全相反的结果,我们可以通过判断三角形三条边与顶点到某点的叉积来判断各自的左右关系,当左右关系完全一致则在三角形内。
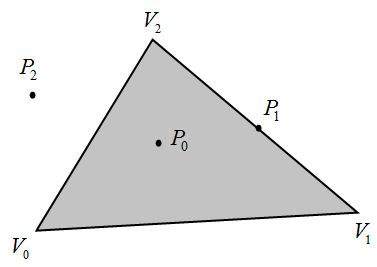
例如此图,$P_0$ 满足 $\vec{V_{0}P_{0}}\times\vec{V_{0}V_{1}}$ / $\vec{V_{1}P_{0}}\times\vec{V_{1}V_{2}}$ / $\vec{V_{2}P_{0}}\times\vec{V_{2}V_{0}}$ 三者同正负,但 $P_1$ / $P_2$ 无法满足这一点。其中 $P_1$ 的叉积会有个是0 ,对于这种线上的情况就看栅格化渲染器自身处理了。
为了优化遍历次数,可以先对三角形做包围盒后在包围盒中便利,对每一行的便利,也可先算出头尾再做遍历。
抗锯齿
由于采样频率小于图像信号频率,会产生锯齿。
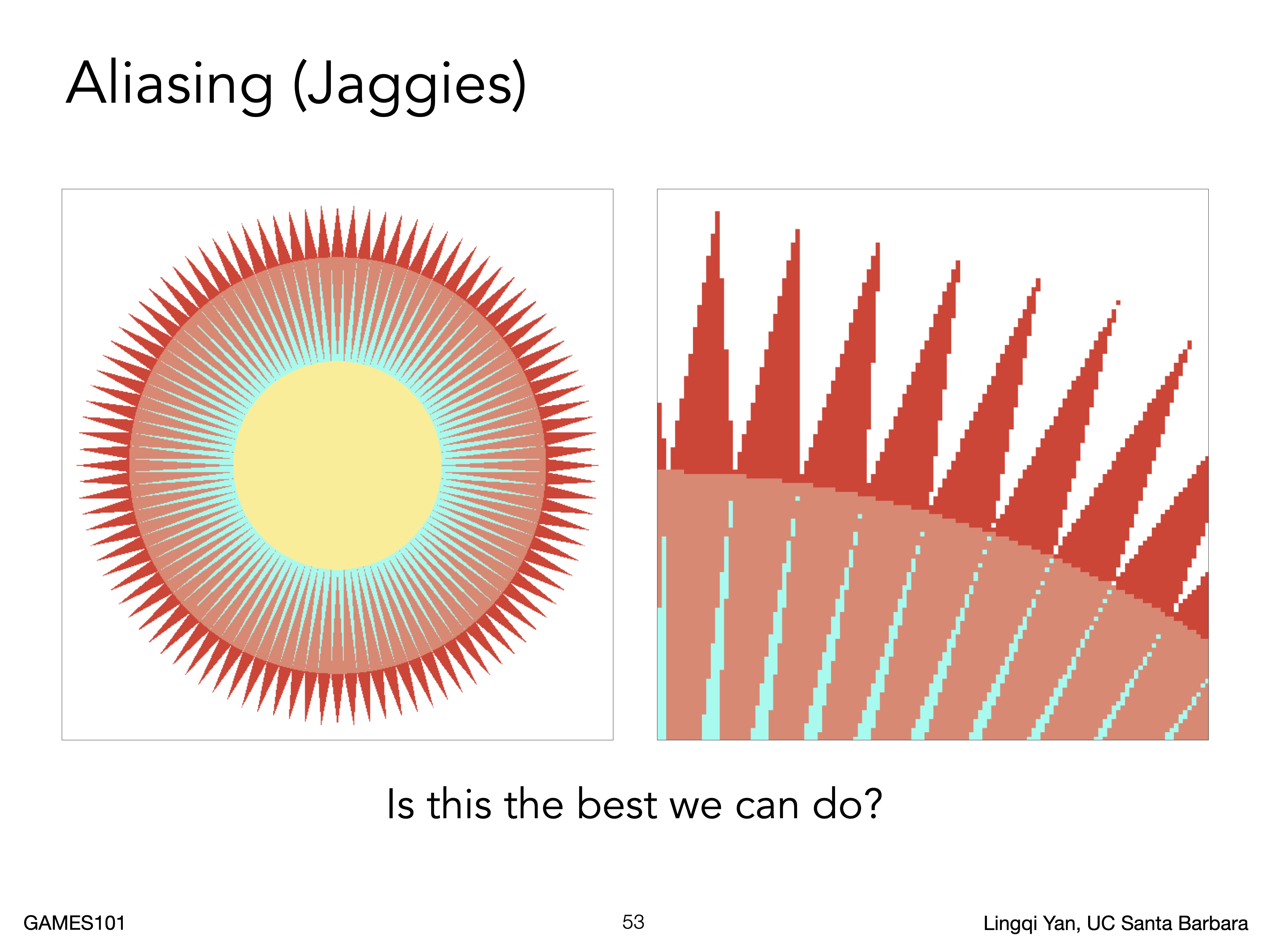
这种失真常发生在物体边缘部分,像素采样对边缘部分高频信号采样不足导致走样。
这有很多种解决办法,相信大家玩游戏的时候也都遇到过(开始抄Wikipedia):
- 超级采样抗锯齿(Super-Sampling Anti-aliasing,简称SSAA);
- 多重采样抗锯齿(Multisampling Anti-Aliasing,简称MSAA)是一种特殊的超级采样抗锯齿(SSAA);
- 覆盖采样抗锯齿(Coverage Sampling Anti-Aliasing,简称CSAA)是nVidia G80系列出现时一并出现的抗锯齿技术;
- 可编程过滤抗锯齿(Custom Filter Anti-Aliasing,简称CFAA)技术起源于AMD-ATI的R600家庭;
- 快速近似抗锯齿(Fast Approximate Anti-Aliasing,简称FXAA)是由Timothy Lottes开发的一种反锯齿;
- 时间混叠抗锯齿(Temporal Anti-Aliasing,简称TXAA)是NVIDIA开发的抗锯齿技术,TXAA是为减少移动时的锯齿现象采用了不同时间帧的像素进行采样,跟前几样空间反锯齿比起来,TXAA大幅减少了移动中的破碎影像;
- 深度学习抗锯齿(Deep Learning Anti-Aliasing,简称DLAA)是利用位于远程的深度学习专用TPU的深度计算性能,预先运算大量的超级取样样本影像,再将样本影像与在本机端即时运算生成的影像进行差异比较,然后通过学习、观察其中的差距,来重新实现完成前者的影像质量,以达到抗锯齿成果,DLAA是一个需要远程资源与本地资源互相配合,协同工作产生抗锯齿效果的抗锯齿技术。
就这样我又水了不少字。都是算力换图像。
举个我写的SSAA例子:
float inside = (float)(
insideTriangle((float)x + 0.0f/2, (float)y + 0.0f/2, v) +
insideTriangle((float)x + 0.0f/2, (float)y + 1.0f/2, v) +
insideTriangle((float)x + 1.0f/2, (float)y + 1.0f/2, v) +
insideTriangle((float)x + 1.0f/2, (float)y + 0.0f/2, v)) / 4.0f;
在一个像素点(x,y)内做了做了四次“是否在三角形内”的判断,最后取得一个系数来取三角形属性。效果如下

这一节课主要讲了信号与系统的知识,在此不做复习。
Z-Buffer
对于多三角形的层叠渲染,这边的Z轴有了作用,用来判断深度。因此也需要多一个图像大小的buffer来存放当前已经算过像素点的深度,用于后续三角形判断是否覆盖。
应该还有更好的方法。
就这?只有颜色?
不不不,懒得写了,下次再写详细的渲染与贴图。